기구학 | 대수적 속도 해석

1. 대수적 속도 해석

   슬라이드-크랭크 기구나 4절 기구와 같은 1자유도의 기구에서 입력 링크의 각속도가 정해지면, 나머지 링크의 회전 속도가 모두 결정된다. 각 링크의 회전 속도는 앞서 계산한 각 링크의 위치나 벡터 방정식을 시간에 대하여 미분하여 구할 수 있으므로, 속도 해석은 언제나 위치 해석이 완료되었다는 가정 하에 수행된다.

 

$$ \begin{align} \omega_{n}=\dot{\theta}_{n}=\frac{d\theta_{n}}{dt} \end{align} $$

 

2. 예제

2.1. 슬라이더-크랭크 기구

 

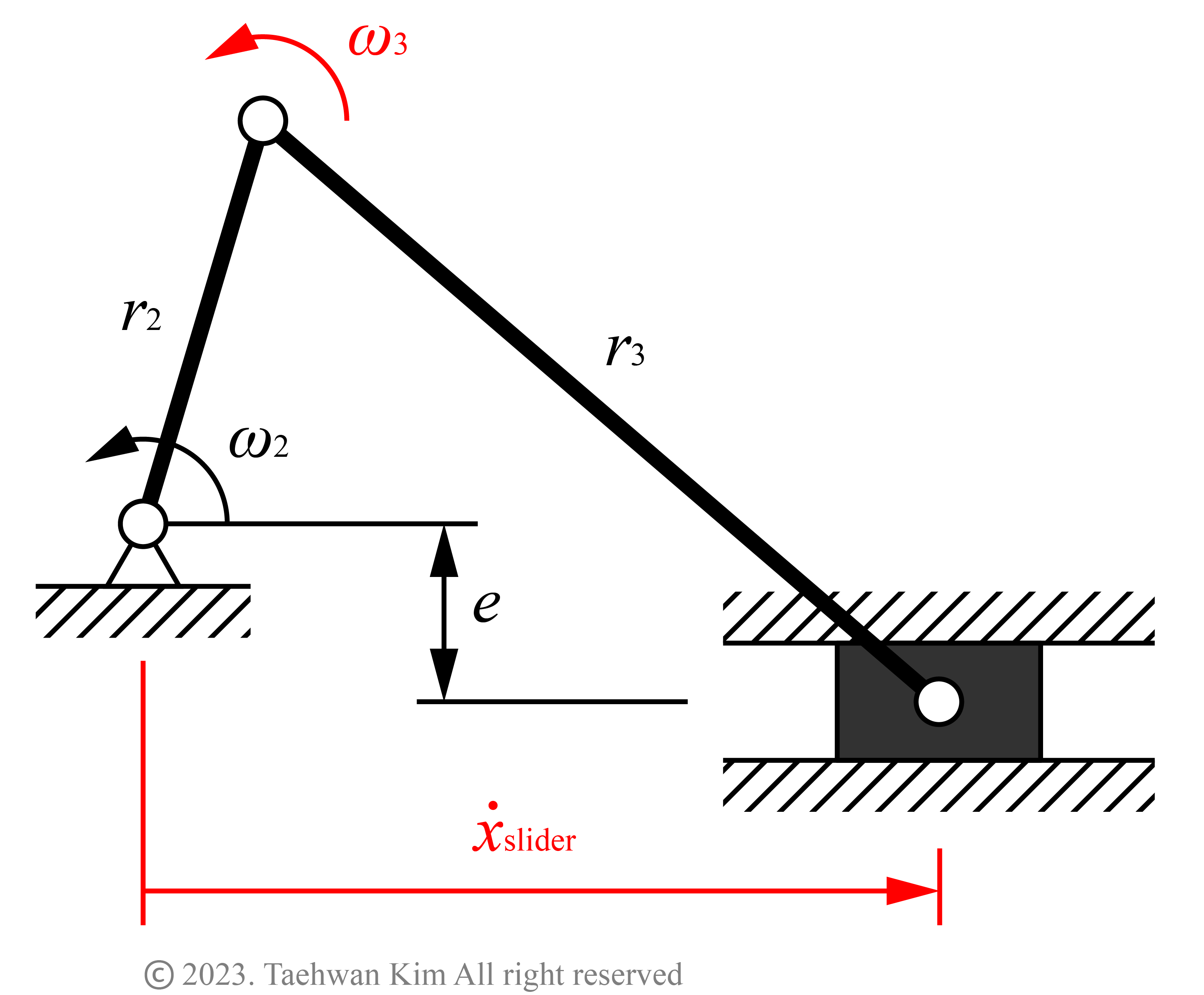
슬라이더-크랭크 기구

   링크의 길이 r₂, r₃, 입력링크의 각속도 ω₂, 크랭크축과 슬라이드축 사이 높이 e가 주어졌다고 가정하자. 커플러 링크의 회전각도 θ₃을 미분하여 각속도를 계산하면 다음과 같다.

 

$$ \begin{align} \theta_{3}&=\arcsin\left(\frac{-r_{2}\sin\theta_{2}-e}{r_{3}}\right)\\\\ \frac{d\theta_{3}}{dt}&=\frac{-r_{2}\cos\theta_{2}}{r_{3}\sqrt{1-\left(\frac{-r_{2}\sin\theta_{2}-d}{r_{3}}\right)^{2}}}\frac{d\theta_{2}}{dt}\\\\ \omega_{3}&=\frac{-r_{2}\omega_{2}\cos\theta_{2}}{r_{3}\sqrt{1-\left(\frac{-r_{2}\sin\theta_{2}-d}{r_{3}}\right)^{2}}} \end{align} $$

 

   다음으로, 크랭크축과 슬라이드 사이 너비 x_slider를 미분하여 슬라이더의 속력을 계산하면 다음과 같다.

 

$$ \begin{align} x_{slider}&=r_{2}\cos\theta_{2}+r_{3}\sqrt{1-\left(\frac{-r_{2}\sin\theta_{2}-e}{r_{3}}\right)^{2}}\\\\ \frac{dx_{slider}}{dt}&=-r_{2}\frac{d\theta_{2}}{dt}\sin\theta_{2}-\frac{r_{2}\left(r_{2}\sin\theta_{2}+e\right)\cos\theta_{2}}{r_{3}\sqrt{1-\left(\frac{-r_{2}\sin\theta_{2}-e}{r_{3}}\right)^{2}}}\frac{d\theta_{2}}{dt}\\\\ \overset{\cdot }{x}_{slider}&=-r_{2}\omega _{2}\sin\theta_{2}-\frac{r_{2}\left(r_{2}\sin\theta_{2}+e\right)\cos\theta_{2}}{r_{3}\sqrt{1-\left(\frac{-r_{2}\sin\theta_{2}-e}{r_{3}}\right)^{2}}}\omega _{2}\\\\ &=-r_{2}\omega _{2}\left(\sin\theta_{2}+\frac{\left(r_{2}\sin\theta_{2}+e\right)\cos\theta_{2}}{r_{3}\sqrt{1-\left(\frac{-r_{2}\sin\theta_{2}-e}{r_{3}}\right)^{2}}}\right) \end{align} $$

 

2.2. 크랭크-로커 기구

 

크랭크-로커 기구

   입력축과 출력축 사이 거리 r₁, 링크의 길이 r₂, r₃, r₄, 입력링크의 각속도 ω₂가 주어졌다고 가정하자. 위 그림에서 벡터 R₁, R₂, R₃, R₄에 대하여 벡터 방정식을 세운 뒤 풀어내면 다음과 같다.

 

$$ \begin{align} \overrightarrow{R_{2}}+\overrightarrow{R_{3}}&=\overrightarrow{R_{1}}+\overrightarrow{R_{4}}\\\\ r_{2}e^{j\theta_{2}}+r_{3}e^{j\theta_{3}}&=r_{1}+r_{4}e^{j\theta_{4}} \end{align} $$

 

   위 방정식을 시간에 대하여 미분하여 정리하면 다음과 같다.

 

$$ \begin{align} \overset{\cdot }{r}_{2}e^{j\theta_{2}}+jr_{2}\overset{\cdot }{\theta}_{2}e^{j\theta_{2}}+\overset{\cdot }{r}_{3}e^{j\theta_{3}}+jr_{3}\overset{\cdot }{\theta}_{3}e^{j\theta_{3}}&=\overset{\cdot }{r}_{1}+\overset{\cdot }{r}_{4}e^{j\theta_{4}}+jr_{4}\overset{\cdot }{\theta}_{4}e^{j\theta_{4}}\\\\ jr_{2}\overset{\cdot }{\theta}_{2}e^{j\theta_{2}}+jr_{3}\overset{\cdot }{\theta}_{3}e^{j\theta_{3}}&=jr_{4}\overset{\cdot }{\theta}_{4}e^{j\theta_{4}}\\\\ jr_{2}\omega_{2}e^{j\theta_{2}}+jr_{3}\omega _{3}e^{j\theta_{3}}&=jr_{4}\omega_{4}e^{j\theta_{4}}\\\\ jr_{2}\omega_{2}\left(\cos\theta_{2}+j\sin\theta_{2}\right)+jr_{3}\omega_{3}\left(\cos\theta_{3}+j\sin\theta_{3}\right)&=jr_{4}\omega_{4}\left(\cos\theta_{4}+j\sin\theta_{4}\right)\\\\ jr_{2}\omega_{2}\cos\theta_{2}-r_{2}\omega_{2}\sin\theta_{2}+jr_{3}\omega_{3}\left(\cos\theta_{3}+j\sin\theta_{3}\right)&=jr_{4}\omega_{4}\cos\theta_{4}-r_{4}\omega_{4}\sin\theta_{4} \end{align} $$

 

   위 방정식을 실수부와 허수부로 나누어 연립방정식을 구성하면 다음과 같다.

 

$$ \begin{align} r_{2}\omega_{2}\sin\theta_{2}+r_{3}\omega_{3}\sin\theta_{3}&=r_{4}\omega_{4}\sin\theta_{4}\\\\ r_{2}\omega_{2}\cos\theta_{2}+r_{3}\omega_{3}\cos\theta_{3}&=r_{4}\omega_{4}\cos\theta_{4}\\\\ \\\\ r_{3}\omega_{3}\sin\theta_{3}-r_{4}\omega_{4}\sin\theta_{4}&=-r_{2}\omega_{2}\sin\theta_{2}\\\\ r_{3}\omega_{3}\cos\theta_{3}-r_{4}\omega_{4}\cos\theta_{4}&=-r_{2}\omega_{2}\cos\theta_{2}\\\\ \\\\ \begin{bmatrix} r_{3}\sin\theta_{3} & -r_{4}\sin\theta_{4} \\ r_{3}\cos\theta_{3} & -r_{4}\cos\theta_{4} \\ \end{bmatrix} \begin{bmatrix} \omega_{3} \\ \omega_{4} \end{bmatrix} &= \begin{bmatrix} -r_{2}\omega_{2}\sin\theta_{2} \\ -r_{2}\omega_{2}\cos\theta_{2} \end{bmatrix} \end{align} $$

 

   위 연립방정식으로부터 커플러 링크의 각속도 ω₃과 출력링크의 각속도 ω₄를 구하면 다음과 같다.

 

$$ \begin{align} \begin{bmatrix} \omega_{3} \\ \omega_{4} \end{bmatrix} &= \begin{bmatrix} r_{3}\sin\theta_{3} & -r_{4}\sin\theta_{4} \\ r_{3}\cos\theta_{3} & -r_{4}\sin\theta_{4} \\ \end{bmatrix}^{-1} \begin{bmatrix} -r_{2}\omega_{2}\sin\theta_{2} \\ -r_{2}\omega_{2}\cos\theta_{2} \end{bmatrix}\\\\ &= \frac{1}{-r_{3}r_{4}\sin\theta_{3}\cos\theta_{4}+r_{3}r_{4}\cos\theta_{3}\sin\theta_{4}} \begin{bmatrix} -r_{4}\sin\theta_{4} & r_{4}\sin\theta_{4} \\ -r_{3}\cos\theta_{3} & r_{3}\sin\theta_{3} \\ \end{bmatrix} \begin{bmatrix} -r_{2}\omega_{2}\sin\theta_{2} \\ -r_{2}\omega_{2}\cos\theta_{2} \end{bmatrix}\\\\ &= \frac{1}{r_{3}r_{4}\sin\left(\theta_{4}-\theta_{3}\right)} \begin{bmatrix} r_{2}r_{4}\sin\theta_{2}\cos\theta_{4}-r_{2}r_{4}\cos\theta_{2}\sin\theta_{4} \\ r_{2}r_{3}\sin\theta_{2}\cos\theta_{3}-r_{2}r_{3}\cos\theta_{2}\sin\theta_{3} \end{bmatrix}\\\\ &= \frac{1}{r_{3}r_{4}\sin\left(\theta_{4}-\theta_{3}\right)} \begin{bmatrix} r_{2}r_{4}\sin\left(\theta_{2}-\theta_{4}\right)\omega_{2} \\ r_{2}r_{3}\sin\left(\theta_{2}-\theta_{3}\right)\omega_{2} \end{bmatrix} \end{align} $$

 

$$ \begin{align} \omega_{3}=\frac{r_{2}\sin\left(\theta_{2}-\theta_{4}\right)}{r_{3}\sin\left(\theta_{4}-\theta_{3}\right)}\omega_{2}, \qquad \omega_{4}=\frac{r_{2}\sin\left(\theta_{2}-\theta_{3}\right)}{r_{4}\sin\left(\theta_{4}-\theta_{3}\right)}\omega_{2} \end{align} $$

 

 

 

 

 

[함께 읽으면 좋은 페이지]

 

기구학 | 대수적 가속도 해석

기구학: 운동계수를 이용한 대수적 속도/가속도 해석

 

 

 

 

 

참고문헌

- 유홍희. (2014). 기구학. KOCW. http://www.kocw.net/home/cview.do?cid=a86afecc7d028380. 2023.05.28

- Erdman, A. G., and Sandor, G. N. (1997). Mechanism Design: Analysis and Synthesis (Vol. 1). Prentice-Hall, Inc.