최적설계 | 카루시-쿤-터커 KKT 최적성 조건(2)

1. KKT 최적성 조건의 대안 형식

   앞서 소개한 KKT 최적성 조건에서 부등호제약조건을 완화변수 없이 나타내보자. 표준화된 최적화 문제를 완화변수 없이 라그랑주 함수로 나타내면 다음과 같다.
 

$$ \begin{align} L \left( \textbf{x} \right) &= f\left ( \textbf{x} \right)+\sum_{i=1}^{p}v_{i}h_i\left( \textbf{x} \right)+\sum_{j=1}^{m}u_{j} g_{j}\left ( \textbf{x} \right ) \\\\ &=f\left ( \textbf{x} \right ) + \textbf{v}^{T}\mathbf{h}\left ( \textbf{x} \right ) + \textbf{u}^{T} \mathbf{g}\left ( \textbf{x} \right ) \end{align}$$

 
   라그랑주 함수를 이용해 국소적 최소점 후보군이 되기 위한 필요조건을 표현하면 다음과 같다.
  

$$ \begin{align} \frac{\partial L \left( \mathbf{x^*} \right) }{\partial x_k} &=0;~~~~k=1~to~n\\\\ h_i \left( \mathbf{x^*} \right) &=0;~~~~i=1~to~p\\\\ g_j \left( \mathbf{x^*} \right) &\leq 0;~~~~j=1~to~m\\\\ u_j^{*}g_j \left( \mathbf{x^*} \right) &= 0;~~~~j=1~to~m \end{align}$$

 

2. 2계 필요조건

   앞서 비제약조건 문제에서 살펴보았던 것처럼, 국소적 최소점 후보군 중 어느 설계변수벡터가 국소적 최소점인지 알기 위해서는 2계 필요조건을 살펴보아야 한다. 비제약조건 문제에서 국소적 충분조건은 최적해에서 목적함수를 테일러 급수 전개했을 때, 0이 아닌 모든 변화량벡터에 대해 이차항이 양수가 되어야 한다는 것이다. 제약조건 문제에서는 변화량벡터를 결정하기 위해 최적해에서의 활성제약조건을 고려해야 한다. 활성제약조건을 만족하는 변화량벡터는 활성제약조건의 경사도와 직교한다. 따라서 등호제약조건과 부등호제약조건의 경사도와 변화량벡터의 내적은 다음과 같이 0이어야 한다.

 

$$ \triangledown h_i^T \left( \mathbf{x^*} \right) \mathbf{d}=0,~~~~ \triangledown g_j^T \left( \mathbf{x^*} \right) \mathbf{d}=0 $$

 

   위 방정식은 최적해에서 변화량벡터를 결정하는 데 사용된다. 이때 활성 부등호제약조건만이 변화량벡터를 결정하는 데 이용된다는 것을 주의하자. 2계 조건을 유도하기 위해서 라그랑주 함수의 테일러 급수 전개식을 쓰고 위 방정식을 만족하는 변화량벡터만을 고려한다. 테일러 전개에서 이차항이 앞서 구한 모든 변화량벡터에 대해 양수이면 해당 설계변수벡터는 국소적 최소점이다. 이를 수식으로 나타내기 위해 최적해에서 라그랑주 함수의 헷세행렬을 다음과 같이 정의할 수 있다.

 

$$ \triangledown^2 L \left( \mathbf{x^*} \right) = \triangledown^2 f \left( \mathbf{x^*} \right) + \sum_{i=1}^{p} v_j^* \triangledown^2h_i \left( \mathbf{x^*} \right) + \sum_{j=1}^{m} u_j^* \triangledown^2g_j \left( \mathbf{x^*} \right) $$

   만일 해당 국소점 최소점의 후보군이 최적설계문제의 국소적 최소점이라면 다음은 반드시 성립한다. 어떤 점이 2계 필요조건을 만족하지 않는다면 그 점은 국소적 최소점이 될 수 없다.

 

$$ Q=\mathbf{d}^T\triangledown^2 L \left( \mathbf{x^*} \right) \mathbf{d} \geq 0 $$

 

3. 예제

3.1. KKT 최적성 조건의 대안 형식

 

KKT 최적성 조건의 대안 형식

 

    부등호제약조건을 고려하여 아래 목적함수의 국소적 최소점을 찾아보자.

 

$$ \begin{align} f\left ( \textbf{x} \right ) &= x_1^{2}+x_2^{2}-2x_1-2x_2+2\\\\ g_1\left ( \mathbf{x} \right ) &= -2x_1-x_2+4 \leq 0 \\\\ g_2\left ( \mathbf{x} \right ) &= -x_1-2x_2+4 \leq 0 \end{align}$$

   위 최적화 문제를 라그랑주 함수 형태로 표현하면 다음과 같다.
 

$$ \begin{align} L\left ( \mathbf{x} \right ) &= f\left( \mathbf{x} \right) +u_1 g_1\left( \mathbf{x} \right) +u_2 g_2\left( \mathbf{x} \right)\\\\ &=x_1^{2}+x_2^{2}-2x_1-2x_2+2 + u_1 \left( -2x_{1}-x_{2}+4 \right) + u_2 \left( -x_{1}-2x_{2}+4 \right) \end{align}$$

 
   라그랑주 함수를 이용해 국소적 최소점 후보군이 되기 위한 필요조건을 표현하면 다음과 같다.
 

$$ \begin{align} \frac{\partial L \left( \mathbf{x^*} \right) }{\partial x_1} &= 2x_1-2-2u_1-u_2 = 0\\\\ \frac{\partial L \left( \mathbf{x^*} \right) }{\partial x_2} &= 2x_2-2-u_1-2u_2 = 0\\\\ g_1 \left( \mathbf{x^*} \right) &= -2x_1-x_2+4 \leq 0\\\\ g_2 \left( \mathbf{x^*} \right) &= -x_1-2x_2+4 \leq 0\\\\ u_1^{*}g_1 \left( \mathbf{x^*} \right) &= 0\\\\ u_2^{*}g_2 \left( \mathbf{x^*} \right) &= 0 \end{align}$$

 

$$ \begin{flalign} ①~u_1=0,~u_2=0: && \end{flalign} $$

 

$$ \begin{align} &2x_1-2 = 0~~~~\left( x_1=1 \right)\\\\ &2x_2-2 = 0~~~~\left( x_2=1 \right)\\\\\ &g_1 \left( \mathbf{x^*} \right) = 1 > 0~~~~\left( not feasible \right)\\\\ &g_2 \left( \mathbf{x^*} \right) = 1 > 0~~~~\left( not feasible \right) \end{align} $$

 

$$ \begin{flalign} ②~u_1=0,~g_2 \left( \mathbf{x^*} \right) =0: && \end{flalign} $$

 

$$ \begin{align} & 2x_1-2-u_2 = 0~~~~\left(x_1=\frac{1}{2}u_2+1 \right)\\\\ & 2x_2-2-2u_2 = 0~~~~\left(x_2=u_2+1 \right)\\\\ & -x_1-2x_2+4 = 0\\\\ \\\\ & -\frac{5}{2}u_2+1 = 0~~~~\left( u_2=\frac{2}{5} \right)\\\\ \\\\ & g_1 \left( \mathbf{x^*} \right) = \frac{1}{5} > 0~~~~\left( not feasible \right) \end{align} $$

 

$$ \begin{flalign} ③~g_1 \left( \mathbf{x^*} \right) =0,~u_2=0: && \end{flalign} $$

 

$$ \begin{align} & 2x_1-2-2u_1 = 0~~~~\left(x_1=u_1+1 \right)\\\\ & 2x_2-2-u_1 = 0~~~~\left(x_2=\frac{1}{2}u_1+1 \right)\\\\ & -2x_1-x_2+4 = 0\\\\ \\\\ & -\frac{5}{2}u_1+1=0~~~~\left( u_2=\frac{2}{5} \right)\\\\ \\\\ & g_2 \left( \mathbf{x^*} \right) = \frac{1}{5} > 0~~~~\left( not feasible \right) \end{align} $$

 

$$ \begin{flalign} ④~g_1 \left( \mathbf{x^*} \right) =0,~g_2 \left( \mathbf{x^*} \right) =0: && \end{flalign} $$

 

$$ \begin{align} & 2x_1-2-2u_1-u_2 = 0\\\\ & 2x_2-2-u_1-2u_2 = 0\\\\ & -2x_1-x_2+4 = 0\\\\ & -x_1-2x_2+4 = 0\\\\ \\\\ & \frac{2}{3}-2u_1-u_2 = 0\\\\ & \frac{2}{3}-u_1-2u_2 = 0\\\\ & x_1 = \frac{4}{3},~~~~x_2=\frac{4}{3}\\\\ \\\\ & u_1 = \frac{2}{9} \geq 0,~~~~u_2=\frac{2}{9} \geq 0\\\\ \end{align} $$

 

$$ \begin{align} \therefore~ u_1^{*}=\frac{2}{9},~~~~ u_2^{*}=\frac{2}{9},~~~~ x_{1}^{*}=\frac{4}{3},~~~~x_{2}^{*}=\frac{4}{3} \end{align} $$

 

3.2. 2계 필요조건

 

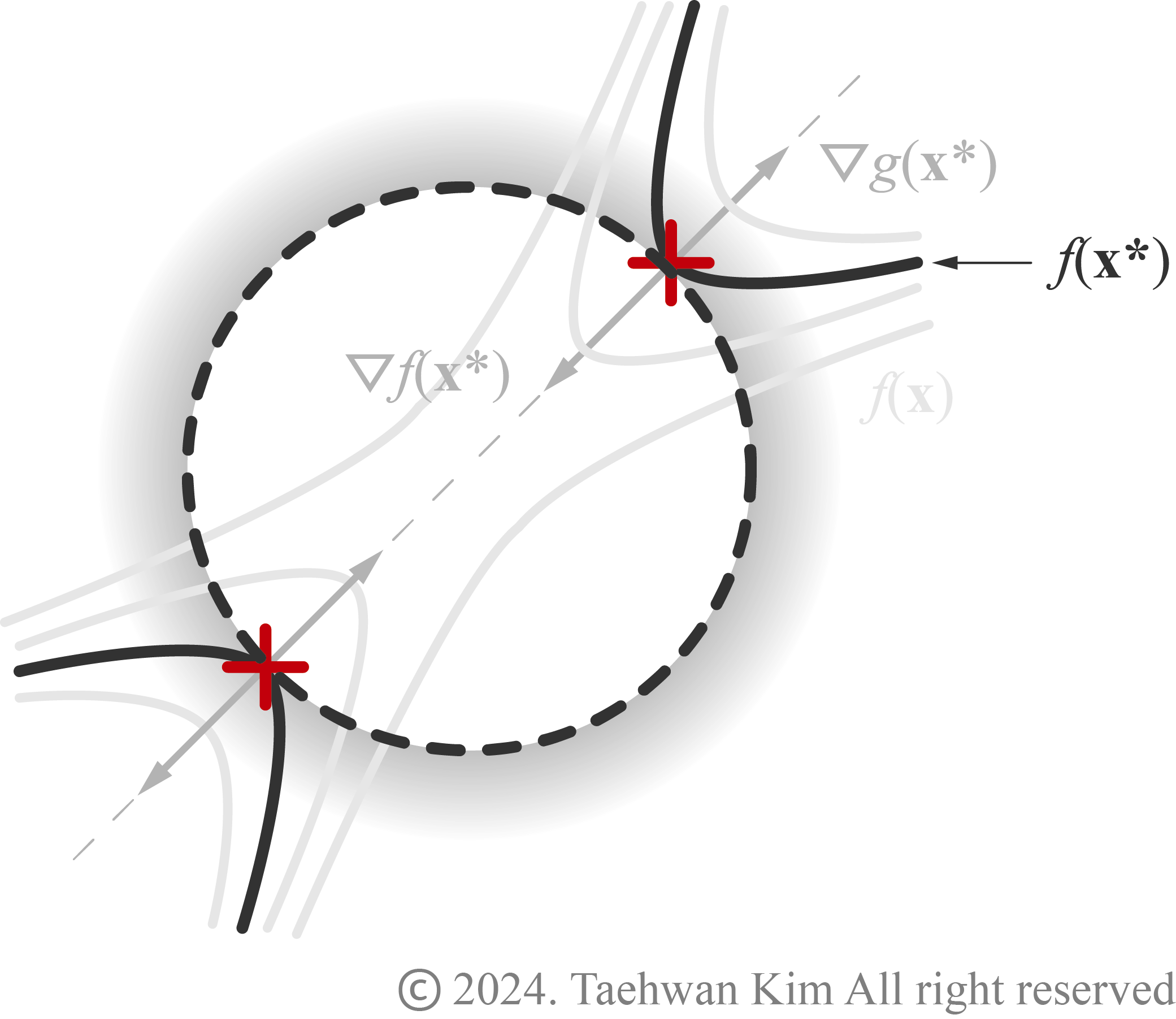
2계 필요조건

    부등호제약조건을 고려하여 아래 목적함수의 국소적 최소점을 찾아보자.

 

$$ \begin{align} f\left ( \textbf{x} \right ) &= x_1^{2}+x_2^{2}-3x_1x_2\\\\ g\left ( \mathbf{x} \right ) &= x_1^{2}+x_2^{2}-6 \leq 0 \end{align}$$

   위 최적화 문제를 라그랑주 함수 형태로 표현하면 다음과 같다.
 

$$ \begin{align} L\left ( \mathbf{x} \right ) &= f\left( \mathbf{x} \right) +u g\left( \mathbf{x} \right)\\\\ &=x_1^{2}+x_2^{2}-3x_1x_2 + u \left( x_1^{2}+x_2^{2}-6 \right) \end{align}$$

 
   라그랑주 함수를 이용해 국소적 최소점 후보군이 되기 위한 필요조건을 표현하면 다음과 같다.
 

$$ \begin{align} \frac{\partial L \left( \mathbf{x^*} \right) }{\partial x_1} &= \left( 2+2u \right) x_1 -3x_2 = 0\\\\ \frac{\partial L \left( \mathbf{x^*} \right) }{\partial x_2} &= -3x_1 + \left( 2+2u \right) x_2 = 0\\\\ g \left( \mathbf{x^*} \right) &= x_1^2 + x_2^2 - 6 \leq 0\\\\ u^{*} g \left( \mathbf{x^*} \right) &= 0 \end{align}$$

 

$$ \begin{flalign} ①~u=0: && \end{flalign} $$

 

$$ \begin{align} &2x_1-3x_2 = 0\\\\ &-3x_1+2x_2 = 0\\\\ \\\\ &x_1=0,~x_2=0\\\\ &g \left( \mathbf{x^*} \right) = -6 \leq 0 \end{align} $$

 

$$ \begin{align} \therefore~ u^{*}=0,~~~~ x_{1}^{*}=0,~~~~x_{2}^{*}=0 \end{align} $$

 

$$ \begin{flalign} ②~g \left( \mathbf{x^*} \right) =0: && \end{flalign} $$

 

$$ \begin{align} & \left(2+2u \right)x_1-3x_2=0\\\\ & -3x_1+\left(2+2u\right)x_2=0\\\\ & x_1^2x_2^2-6=0\\\\ \\\\ & \left(2+2u-3 \right) x_1+ \left(2+2u-3 \right) x_2 = 0\\\\ \\\\ & \left(2u-1 \right) \left(x_1+x_2 \right) = 0~~~~\left( ⓐ~u=\frac{1}{2},~~~~or~~~~ⓑ~x_1=-x_2 \right) \end{align} $$

 

$$ \begin{flalign} ~~~~ⓐ~u=\frac{1}{2}: && \end{flalign} $$

 

$$ \begin{align} & 3x_1-3x_2=0\\\\ & -3x_1+3x_2=0~~~~\left( x_1=x_2 \right)\\\\ \\\\ & 2x_1^2-6=0~~~~\left(x_1=x_2=\pm\sqrt{3}\right) \end{align} $$

 

$$ \begin{align} \therefore~ u^{*}=\frac{1}{2},~~~~ x_{1}^{*}=\pm\sqrt{3},~~~~x_{2}^{*}=\pm\sqrt{3} \end{align} $$

 

$$ \begin{flalign} ~~~~ⓑ~x_1=-x_2: && \end{flalign} $$

 

$$ \begin{align} & 2x_1^2-6=0~~~~\left(x_1=-x_2=\pm\sqrt{3}\right)\\\\ \\\\ & \left(2+2u\right)x_1+3x_1=0\\\\ & 5+2u=0\\\\ & u=-\frac{5}{2} < 0~~~~\left(not~feasible\right) \end{align} $$

 

   앞서 구한 국소적 최소점 후보군 중 어느 설계변수벡터가 국소적 최소점인지 알기 위해 2계 필요조건을 살펴보자. 목적함수와 제약조건함수의 헷세행렬과 라그랑주 함수의 헷세 행렬은 다음과 같다.

 

$$ \begin{align} \triangledown^2 f &= \begin{bmatrix} 2 & -3 \\ -3 & 2 \\ \end{bmatrix}\\\\ \triangledown^2 g &= \begin{bmatrix} 2 & 0 \\ 0 & 2 \\ \end{bmatrix}\\\\ \triangledown^2 L &= \triangledown^2 f + u\triangledown^2 g = \begin{bmatrix} 2+2u & -3 \\ -3 & 2+2u \\ \end{bmatrix} \end{align} $$

 

$$ \begin{flalign} ①~u^*=0,~~~~x_1^*=0,~~~~x_2^*=0: && \end{flalign} $$

 

$$ \begin{align} & \triangledown^2 L = \begin{bmatrix} 2 & -3 \\ -3 & 2 \\ \end{bmatrix}\\\\ \\\\ & \begin{vmatrix} 2-\lambda & -3 \\ -3 & 2-\lambda \\ \end{vmatrix}=\left( 2-\lambda \right)^2-9 = \lambda^2-4\lambda-5 = \left(\lambda+1\right)\left(\lambda-5\right)=0\\\\ \\\\ & \lambda_1=-1,~~~~\lambda_2=5~~~~\left(not~positive~definite\right) \end{align} $$

 

$$ \begin{flalign} ②~u^*=\frac{1}{2}0,~~~~x_1^*=\pm\sqrt{3},~~~~x_2^*=\pm\sqrt{3}: && \end{flalign} $$

 

$$ \begin{align} & \triangledown^2 L = \begin{bmatrix} 3 & -3 \\ -3 & 3 \\ \end{bmatrix}\\\\ \\\\ & \begin{vmatrix} 3-\lambda & -3 \\ -3 & 3-\lambda \\ \end{vmatrix}=\left( 3-\lambda \right)^2-9 = \lambda^2-6\lambda = \lambda\left(\lambda-6\right)=0\\\\ \\\\ & \lambda_1=0,~~~~\lambda_2=6~~~~\left(postive~semidefinite\right) \end{align} $$

 

    라그랑주 함수의 헷세행렬이 양정이 아닌 양반정이므로, 다음을 만족하는 변화량벡터를 구하고 2계 필요조건을 살펴보자.

 

$$ \begin{align} \triangledown g^T \left( \mathbf{x} \right) \mathbf{d} &= \begin{bmatrix} 2x_1^* & 2x_2^* \end{bmatrix} \begin{bmatrix} d_1 \\ d_2 \end{bmatrix} \\\\ &=\pm 2\sqrt{3} \begin{bmatrix} 1 & 1 \end{bmatrix} \begin{bmatrix} d_1 \\ d_2 \end{bmatrix} \\\\ &=\pm 2\sqrt{3} \left( d_1+d_2 \right) \\\\ &= 0~~~~\left( d_1=-d_2 \neq 0 \right) \end{align} $$

 

$$ \begin{align} Q &= \mathbf{d}^T \triangledown^2L \left( \mathbf{x^*}\right) \mathbf{d} \\\\ &= \begin{bmatrix} d_1 & -d_1 \end{bmatrix} \begin{bmatrix} 3 & -3 \\ -3 & 3 \end{bmatrix} \begin{bmatrix} d_1 \\ -d_1 \end{bmatrix} \\\\ &= 12d_1^2 > 0 \end{align} $$

 

$$ \begin{align} \therefore~x_1^*=\pm\sqrt{3},~~~~x_2^*\pm\sqrt{3}~~~~\left( local~minimum \right) \end{align} $$

 

 

 

 

 

[함께 읽으면 좋은 페이지]

 

최적설계 | 등호제약조건 문제

최적설계 | 부등호제약조건 문제

최적설계 | 카루시-쿤-터커 KKT 최적성 조건(1)

 

 

 

 

 

참고문헌
- Arora, J. S. (2016). Introduction to optimum design. Elsevier.