최적설계 | 심플렉스법(1)

1. 선형계획문제의 볼록성

선형계획문제의 볼록성

   일반적인 최적설계문제에서 등호제약조건이 선형이고 부등호제약조건이 볼록이면, 해당 설계문제의 유용집합은 볼록집합이다. 만약 해당 유용집합 내에서 도출한 설계대안이 국소적 최소라면, 해당 설계대안은 전역적 최소이다. 선형계획문제에서는 모든 함수가 선형이므로 선형계획문제는 볼록집합이며, 하나의 국소적 최적이 존재한다면 해당 설계대안이 전역적 최적해이다. 또한 선형계획문제에서의 최적해는 항상 유용영역의 경계 부분, 특히 유용영역의 꼭짓점 중 하나에 존재한다. 이는 최적해가 유용영역의 내부에도 존재할 수 있는 일반적인 비선형문제와는 다르다는 것을 보여준다.

 

2. 선형계획문제의 기저해

   표준선형계획문제는 일반적으로 등호제약조건의 수보다 설계변수의 수가 많아 무한 가지의 설계대안이 도출된다. 이때 설계변수의 수와 등호제약조건의 수의 차이만큼에 해당하는 설계변수를 0으로 두고 선형방정식을 풀어 유한 가지의 설계대안을 도출할 수 있다. 이렇게 도출한 해를 기저해(basic solution)라고 부르며,  0으로 두었던 설계변수를 비기저해(nonbasic solution)라고 부른다. 선형계획문제에서 유용영역의 꼭지점은 기저해에 해당하며, 최적해(optimum basic solution)는 이러한 기저해 중에서 최적의 목적함수 값을 갖는 해에 해당한다. 선형계획문제를 손쉽게 다루기 위해서는 유용영역의 꼭짓점에 해당하는 기저해 중에서 최적해를 탐색하도록 문제를 축소할 필요가 있다. n개의 설계변수와 m개의 등호제약조건을 갖는 표준선형계획문제에 대해서 기저해의 최대 수 N은 다음과 같이 계산할 수 있다.

 

$$\begin{array}{r}N=(\genfrac{}{}{0ex}{}{n}{m})=\frac{n!}{m!(n-m)!}\end{array}$$

 

3. 심플렉스법

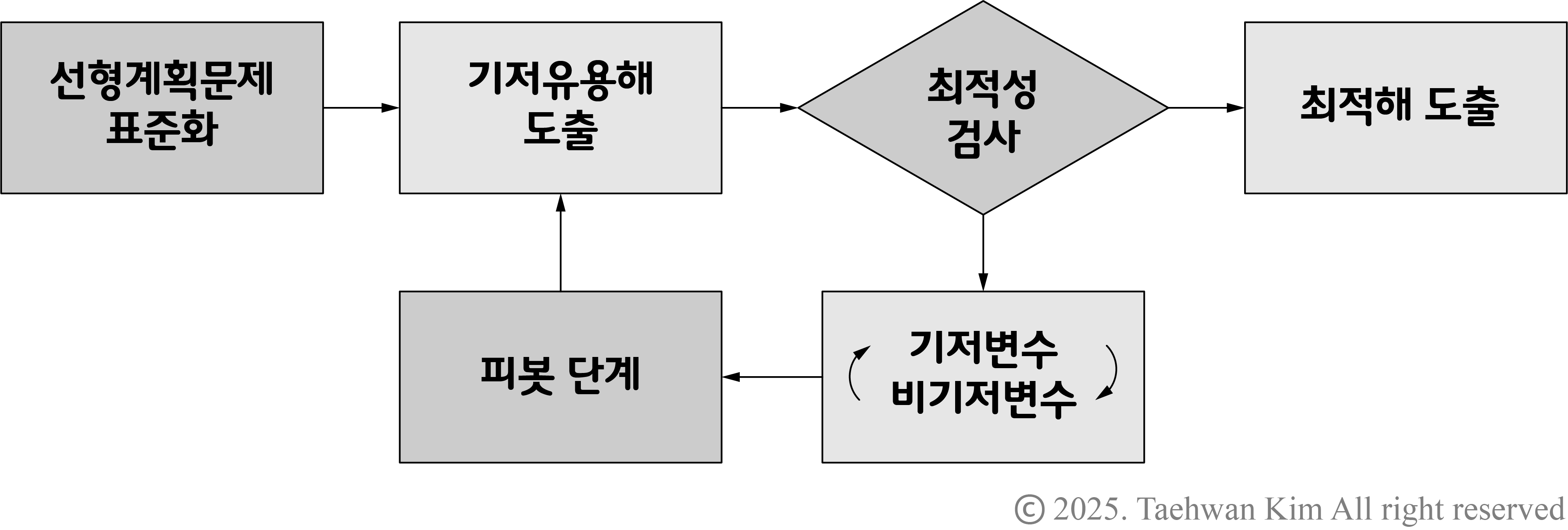
심플렉스법

   심플렉스법은 하나의 기저해에서 시작하여 목적함수를 최소화하는 방향으로 최적해에 도달할 때까지 기저해를 탐색하는 방법이다. 가우스-조던 소거법의 피봇 단계를 통해 현재의 비기저변수와 기저변수를 서로 바꾸어가면서 탐색을 수행한다. 심플렉스법은 유용(feasible)하지 않은 기저해, 즉 설계변수가 음수인 기저해는 탐색하지 않는다. 따라서 심플렉스법을 적용하기에 앞서 반드시 하나의 기저유용해(feasible basic solution)를 가지고 있어야 하며, 현재 기저유용해에서 기저변수를 비기저변수로 대치하여 다음 기저유용해로 이동한다. 그렇다면 빠른 탐색을 위해 어떤 기저변수를 비기저변수로, 어떤 비기저변수를 기저변수로 만들어야 할까?

 

3.1. 기저유용해의 최적성 검사

   심플렉스 단계를 시작할 때 목적함수 또는 가격함수는 반드시 비기저변수로 표현되어야 한다. 이때 가격함수에서 비기저변수의 계수를 환산가격계수(reduced cost coefficients)라 부른다. 모든 환산가격계수가 음이 아니라면, 현재 기저유용해는 최적해에 해당한다.

 

3.2. 기저변수와 비기저변수의 교환

   만약 현재 기저유용해가 최적해가 아니라면 환산가격계수가 음인 경우가 있을 것이다. 이 음의 환산가격계수가 어떤 비기저변수가 가격함수를 줄일 수 있는 기저변수가 될 것인지를 결정한다. 환산가격계수가 음수인 비기저변수 중에서 환산가격계수의 절댓값이 가장 큰 비기저변수를 기저변수로 만들자. 어떤 기저변수를 비기저변수로 만들지 결정하기 위해, 기저해 (또는 등호제약조건에서 우측항에 해당하는 자원한계)들을 기저변수로 만들기로 한 비기저변수의 계수로 나누었을 때 그 값이 음수가 아니면서 가장 작은 기저변수를 비기저변수로 만들자. 변수들을 모두 결정했다면 가우스-조던 소거법을 이용해 기저변수와 비기저변수를 교환한다. 피봇 단계를 통한 기저변수와 비기저변수의 교환 방법은 예제에서 자세하게 다룰 것이다.

 

3.3. 최적해가 여러 개이거나 없는 경우

   비기저변수에 대응하는 환산목적계수가 0이면, 최적값에 변화를 주지 않고 해당 비기저변수를 기저변수로 바꿀 수 있다는 것을 의미한다. 이런 경우에는 목적함수가 제약함수 중의 하나와 평행할 때 나타날 수 있으며, 최적해가 여러 개일 수 있다. 비기저변수에 대응하는 환산목적계수가 음수이더라도, 기저해들을 해당 비기저변수의 계수로 나누었을 때 모든 값이 음수라 더 이상 심플렉스법을 적용할 수 없을 경우에는 모든 제약조건을 만족하는 최적해가 존재하지 않는다. 설계자는 문제의 정식화를 검토하여 너무 과다한 제약조건 혹은 부적당한 정식화가 있는지 점검해야 한다.

 

4. 예제

선형계획문제

   다음과 같이 표준화된 선형계획문제에 심플렉스법을 적용해보자.

 

$$\begin{array}{r}\mathrm{minimize}f=-2x_1-5x_2+5x_3\end{array}$$

 

$$\begin{array}{rl}3x_1+2x_2-2x_3+x_4& =12\\ \\ 2x_1+3x_2-3x_3-x_5& =6\\ \\ x_i\ge 0;i=1& to5\end{array}$$

 

   위 표준선형계획문제를 첨가행렬(augmented matrix)로 정리하면 다음과 같다.

 

$$\begin{array}{r}\left[\begin{array}{cccccc}3& 2& -2& 1& 0& 12\\ 2& 3& -3& 0& -1& 6\\ -2& -5& 5& 0& 0& f\end{array}\right]\end{array}$$

 

   위와 같은 첨가행렬에서 기저변수는 x₄, x₅에 해당하며, 비기저변수는 x₁, x₂, x₃에 해당한다. 해당 설계대안은 x₅의 해가 음수이기 때문에 유용하지 않으므로 심플렉스법을 적용할 수 없다. 기저유용해에 해당하는 첨가행렬을 제시하면 다음과 같다.

 

$$\begin{array}{r}\left[\begin{array}{cccccc}1& \frac{2}{3}& -\frac{2}{3}& \frac{1}{3}& 0& 4\\ 0& -\frac{5}{3}& \frac{5}{3}& \frac{2}{3}& 1& 2\\ 0& -\frac{11}{3}& \frac{11}{3}& \frac{2}{3}& 0& f+8\end{array}\right]\end{array}$$

 

   위 첨가행렬에서 비기저변수 x₂의 환산가격계수가 음수이므로 해당 기저유용해는 최적점이 아니다. 비기저변수 x₂의 환산가격계수가 음수이면서 절댓값이 가장 크고, 기저해를 해당 비기저변수의 계수로 나누었을 때 기저변수 x₁의 값이 음수가 아니면서 가장 작으므로, 기저변수 x₁과 비기저변수 x₂를 교환하여 첨가행렬을 다시 나타내면 다음과 같다.

 

$$\begin{array}{r}\left[\begin{array}{cccccc}\frac{3}{2}& 1& -1& \frac{1}{2}& 0& 6\\ \frac{5}{2}& 0& 0& \frac{3}{2}& 1& 12\\ \frac{11}{2}& 0& 0& \frac{5}{2}& 0& f+30\end{array}\right]\end{array}$$

 

   위 첨가행렬에서 모든 비기저변수의 환산가격계수가 음수가 아니므로 해당 기저유용해가 최적점에 해당한다. 해당 기저유용해에서 가격함수의 값을 계산하면 다음과 같다.

 

$$\begin{array}{rl}\frac{11}{2}{x}_1+\frac{5}{2}{x}_4& =f+30(x_1=0,x_3=0,x_4=0)\\ \\ 0& =f+30\\ \\ \therefore f& =-30\end{array}$$

 

 

 

 

 

[함께 읽으면 좋은 페이지]

 

최적설계 | 심플렉스법(2)

 

 

 

 

 

참고문헌

- Arora, J. S. (2016). Introduction to optimum design. Elsevier.