최적설계 | 비제약조건 문제 수치해법(1): 최속강하법

1. 경사도 기반 수치해법

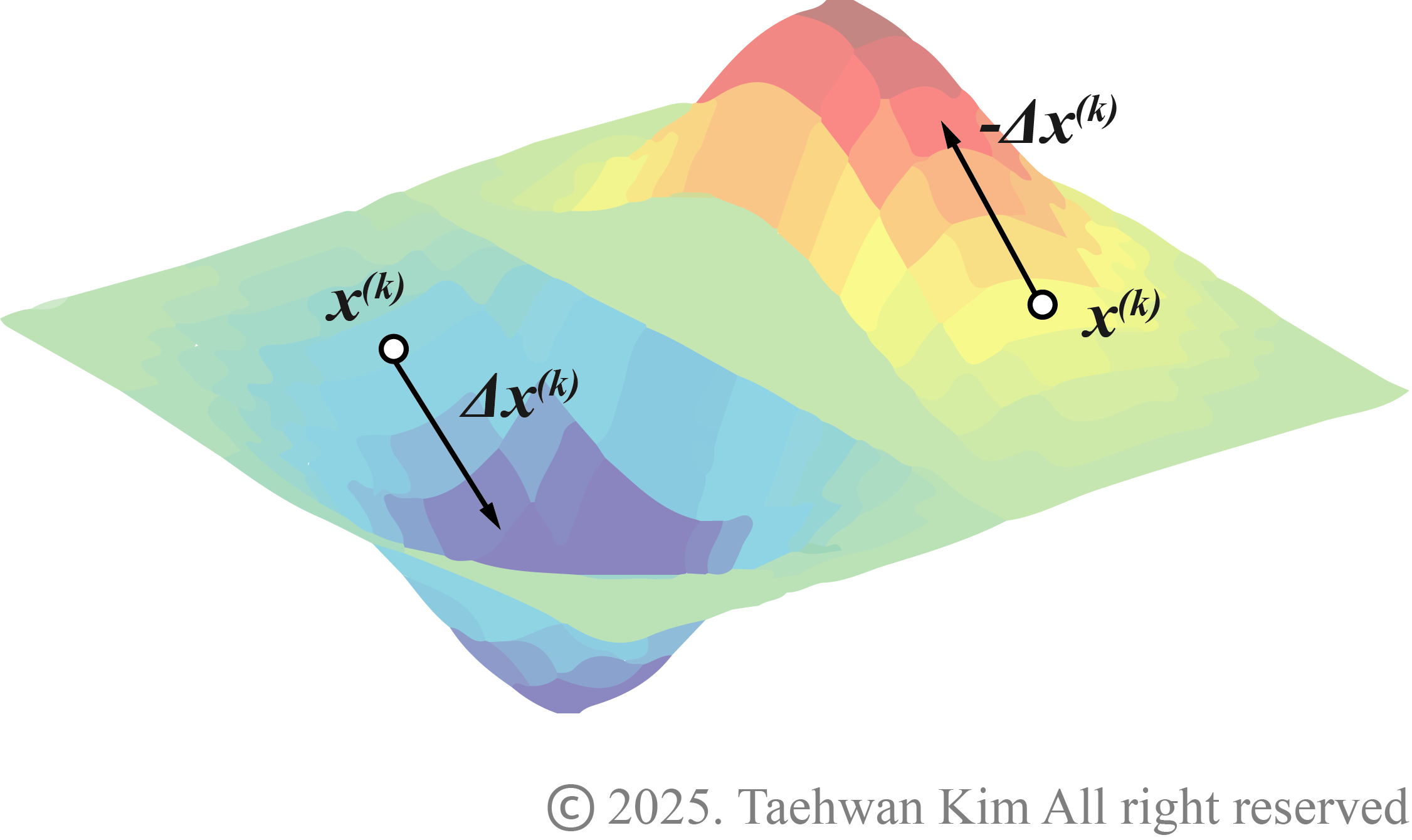
경사도 기반 수치해법

   비선형·비제약조건 최적설계문제는 해석적인 방법으로 다루기에는 다소 무리가 있어, 이를 풀기 위한 수치적 방법들이 개발되었다. 경사도 기반 수치해법은 이러한 문제를 다루는 수치적 방법들 중 가장 기본적인 방법으로, 초기 설계를 시작으로 최적성 조건을 만족할 때가지 동일한 계산을 되풀이하며 국소적 최소점을 탐색한다. 경사도 기반의 최적화 방법은 k+1번째 연산에서 아래와 같은 형식으로 기술된다. 아래와 같이 기술된 반복법은 최적성 조건들을 만족하거나 종료 판정 기준을 충족할 때까지 계속된다. 이 반복 방법은 비선형·비제약조건 문제뿐만 아니라 제약조건 문제에도 적용 가능하다.
 

$$\begin{array}{r}{\mathbf{\text{x}}}^{(k+1)}={\mathbf{\text{x}}}^{\left(k\right)}+\mathrm{\Delta }{\mathbf{\text{x}}}^{\left(k\right)};k=0,1,2,\cdots \end{array}$$

 
   위 형식에서 우변의 두 번째 항에 해당하는 설계 변화량은 다음과 같이 두 부분으로 나눌 수 있다.
 

$$\begin{array}{r}\mathrm{\Delta }{\mathbf{\text{x}}}^{\left(k\right)}={\alpha }_k{\mathbf{\text{d}}}^{\left(k\right)}\end{array}$$

 
   위 식에서 우변의 벡터항은 다음 설계대안을 탐색할 방향, 스칼라항은 탐색방향을 따라 이동할 거리에 해당한다. 탐색방향이 목적함수가 감소하는 방향으로 잘 설정되었다면, 이동거리는 0보다 커야 하므로 양수이다. 설계 변화량을 계산하는 과정은 탐색 방향을 결정하는 문제와 이동거리를 결정하는 문제를 포함한다. 탐색방향과 이동거리를 계산하기 위한 많은 방법들이 있으며, 다양한 조합으로부터 여러 최적화 알고리즘이 개발되었다.
 

2. 최속강하법

   표준화된 최적화 문제의 목표는 목적함수를 최소화하는 것이다. 이를 위해 매 탐색 단계에서 설계변수의 변화는 목적함수가 감소하는 방향으로 향하는 것이 바람직하다. 따라서 탐색 방향을 가리키는 벡터는 다음과 같은 조건을 만족해야 한다. 
 

$$\begin{array}{r}{\mathbf{\text{c}}}^{\left(k\right)}\cdot {\mathbf{\text{d}}}^{\left(k\right)}<0\end{array}$$

   이는 목적함수의 경사도 벡터와 탐색 방향 벡터의 내적이 0보다 작아지도록 탐색 방향을 결정해야 한다는 것을 의미하며, 기하학적으로는 두 벡터가 이루는 각이 둔각이어야 한다. 위 부등식을 만족하는 탐색 방향 벡터를 강하 방향이라고 부르고, 위 부등식을 강하 조건이라고 한다. 이와 같은 최속강하법(steepest gradient descent method)은 현재 단계에서 목적함수의 경사도 정보를 이용하여 목적함수가 가장 빠르게 감소하는 방향을 찾는다. 따라서 해당 문제에서 다루는 모든 함수가 연속이고 미분 가능하다는 가정을 기반으로 한다. 목적함수의 경사도는 다음과 같은 열벡터로 정의된다.
 

$$\begin{array}{r}\mathbf{\text{c}}=▽f={\left[\begin{array}{cccc}\frac{\partial f}{\partial x_1}& \frac{\partial f}{\partial x_2}& \cdots & \frac{\partial f}{\partial x_n}\end{array}\right]}^T\end{array}$$

 
   경사도 벡터는 목적함수가 증가하는 방향을 향하므로, 최대 감소 방향은 해당 방향의 반대 방향이 된다. 그러므로 음의 경사도 벡터는 목적함수에 대한 최속 강하 방향을 나타내고 다음과 같이 결정된다.
 

$$\begin{array}{r}\mathbf{\text{d}}=-\mathbf{\text{c}}=-{\left[\begin{array}{cccc}\frac{\partial f}{\partial x_1}& \frac{\partial f}{\partial x_2}& \cdots & \frac{\partial f}{\partial x_n}\end{array}\right]}^T\end{array}$$

 
   이를 강하 조건에 대입하면, 최속 강하 방향은 아래와 같이 강하 조건을 항상 만족한다는 것을 알 수 있다.
 

$$\begin{array}{r}{\mathbf{\text{c}}}^{\left(k\right)}\cdot {\mathbf{\text{d}}}^{\left(k\right)}=-\Vert {\mathbf{\text{c}}}^{\left(k\right)}\Vert <0\end{array}$$

 

3. 이동거리 결정

   탐색 방향을 결정했다면, 주어진 방향을 따라 얼마나 이동할지 결정한다. 해당 단계에서는 설계변수와 탐색 방향이 결정되어 있으므로 목적함수를 아래와 같은 일변수 함수로 볼 수 있으며, 이때 유일한 미지수는 이동거리이다. 이로써 다변수 최소화 문제가 일변수 최소화 문제로 축소된다.
 

$$\begin{array}{r}f\left({\mathbf{\text{x}}}^{(k+1)}\right)=f({\mathbf{\text{x}}}^{\left(k\right)}+{\alpha }_k{\mathbf{\text{d}}}^{\left(k\right)})=\bar{f}\left({\alpha }_k\right)\end{array}$$

 
   위와 같은 목적함수를 최소화하면 이동거리를 결정할 수 있다. 이때 이동거리를 결정하기 위한 필요조건과 충분조건은 다음과 같다.

 

$$\begin{array}{rl}\frac{\partial \bar{f}\left({\alpha }_k\right)}{\partial \alpha }& =0\\ \\ \frac{{\partial }^2\bar{f}\left({\alpha }_k\right)}{\partial {\alpha }^2}& >0\end{array}$$

 

   목적함수의 형태가 간단하다면 최적성의 필요조건과 충분조건을 사용해 이동거리를 해석적으로 결정하는 것이 가능하다. 하지만 대부분의 문제는 목적함수의 형태가 복잡하기 때문에 이동거리를 해석적으로 결정하기 쉽지 않다. 따라서 수치적으로 이동거리를 결정하여 최적점을 탐색하는 방법들이 고안되었다. 아래 링크로 접속하면 이동거리를 결정하는 다양한 수치 방법론을 확인할 수 있다.

최적설계 | 비제약조건 문제 수치해법(3): 구간감소법

 

4. 최속강하법 알고리즘

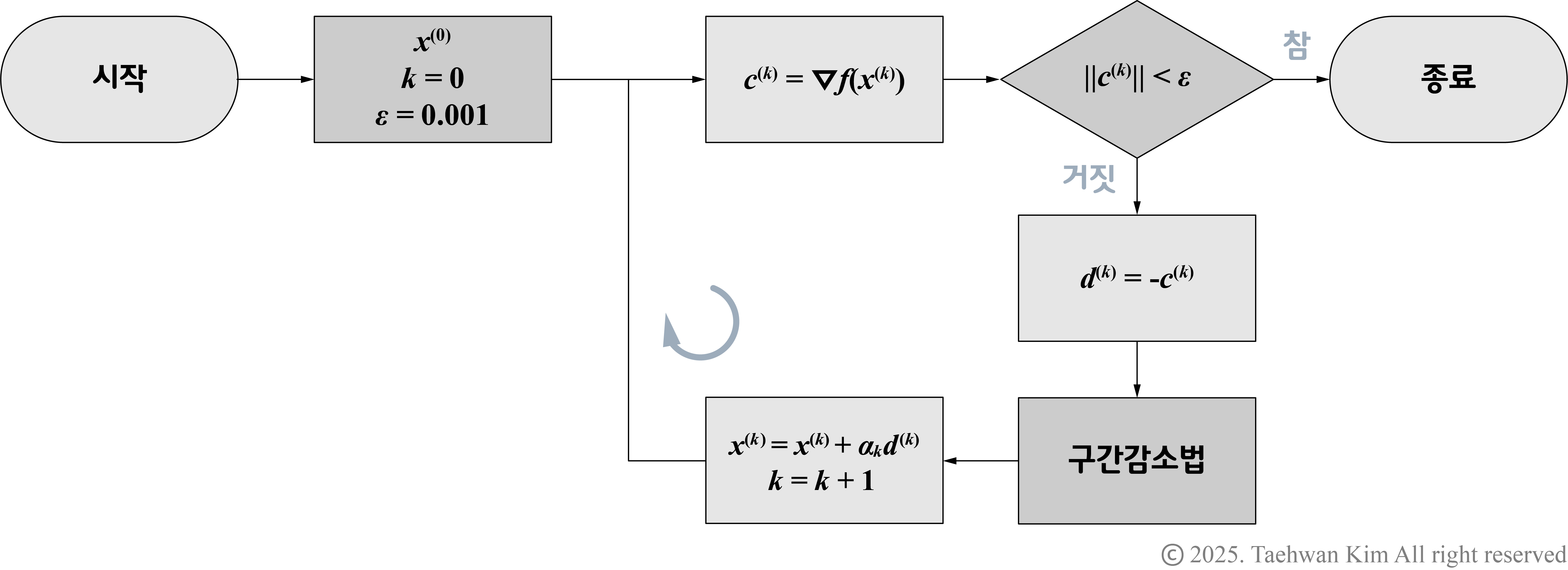
최속강하법 알고리즘

   최속강하법은 초기 설계변수에서 시작한다. 해당 설계변수에서 강하 방향을 정의하고, 그 방향의 절대값이 0이 아니라면 목적함수를 줄이기 위해 해당 방향으로 최대한 멀리 이동한다. 새로운 설계변수를 갱신한 뒤, 해당 설계변수에서 강하 방향을 정의하고 전체 과정을 반복한다. 특정 설계변수 지점에서 경사도의 크기가 허용오차보다 작다면 탐색을 종료한다. 해당 알고리즘은 탐색 과정에서 목적함수 경사도에 대한 국소적인 정보만을 사용하기 때문에 전역적 최소가 아닌 국소적 최소점에 수렴한다.

 

 

 

 

 

[함께 읽으면 좋은 페이지]

 

최적설계 | 비제약조건 문제 수치해법(2): 공액경사법

 

 

 

 

 

참고문헌
- Arora, J. S. (2016). Introduction to optimum design. Elsevier.